Recipe for a Boggled Mind

Here's a good way to boggle your mind. Think about prime numbers. Just think about them, for like 48 hours. It starts off being very strange and difficult. They're just ordinary numbers, right? Numbers that don't happen to be divisible by other natural numbers, save zero and one. The lone pines that stand at odd intervals after the firs have been toppled and chopped up with division lines. Pillars of obstinance in the mess if fickle, irresolute, factorisable integers.

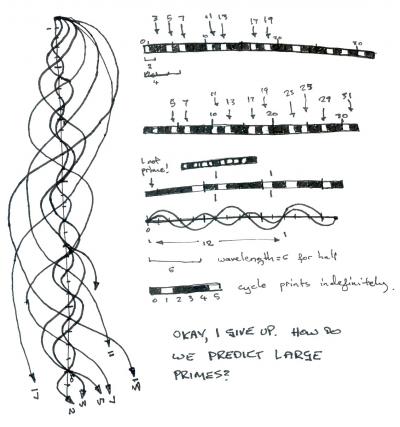
But they're not random. There's a pattern, a clear and bafflingly complex one. A few hours in, you start to notice small things. Only two primes ever touch, two and three. They like to end in 9. They like to end in 3. If you black out the prime multiples one by one you see how it builds up, and where the next prime will be. I thought it was like a wave at first, because I didn't know any better, with each prime adding new curves to the waveform, new harmonics and a multiplied wavelength.

It's not like that. What it is: a developing pattern of gaps, each hole in the pattern of blacked out numbers is a new prime, which blacks out more of the holes ahead of it, making a bigger but perfectly repeating pattern up the number line. It's like a printing wheel that snowballs bigger and bigger as it rolls away from 0. When you see this, you realize why one is not treated as a prime number, I never understood that until now.

Ancient mathematicians knew this and gave it a name, it's called the Sieve of Eratosthenes. This is the same Eratosthenes fellow who devised the latitude and longitude system we use today to navigate the globe, and invented the orrery [flickr] hundreds of years before the Church declared the world flat.

But back to the primes. Once you've watched the wheel turn a few times in your head - and this takes a loooong time - you see how the primes are thinning out as the wheel gets bigger, more primes add more black so the white gaps become sparser. When real mathematicians talk about this they call it the Prime Number Theorem.

Then you realize that the blacked out bits don't much matter, the numbers they cover up are all discarded so the only information is the length of the black bits, the distance between primes. The wheel now shrinks down from a stripey black and white printing press to a small tight wheel of numbers. And still the pattern builds, but you can see it clearly

and... *BANG!* your brain shorts out. You sit in your chair, completely dazed, unable to think about anything. All the understanding, the beauty and form you saw clearly a moment ago is replaced by static.

Bodily functions resume, you suddenly realize you're hungry, thirsty and need to pee. Hours have passed, wince at the time spent when you remember all that you need to get done.

But it's not entirely wasted. If a computer program can be written to efficiently draw the wheel as it grows, up to a list of gap lengths a few gigabytes long then a list of the first x many primes can be made in short order. I fancy it can be done. Once we have the primes we can maybe make a program to create rough rules that prove a large number is not divisible by that prime, or pattern of primes, allowing the rapid elimination of huge swaths of prime factors by a logical tree. It doesn't have to prove if it is divisible, just cut down most of the numbers we might have to test.

Simple example, say 5. Compare to your number to factorize, does that number end in 5 or 0? no? Then it's not divisible by 5. Or 15, 25, 3214320985, etc. One logical rule that nixes a great many numbers we'd have to consider as factors. Thus the program imputes a decision tree for arriving at a small number of candidate primes, which are easily checked against the number we wish to factorize, and factorize but Foxtrot Oscar quickly. We allow perhaps a terabyte, or as much space as we can get, for this tree, and it can process all numbers below a limit of the largest prime squared, producing either the
factors or quickly telling us if the large number is yet another prime. We're sacrificing computational simplicity in exchange for computation time on a grand scale, and automating that.

Sooo... what? The factoring problem is one of the great, some say intractable, problems of mathematics. Being able to factorize large numbers would be a kind of comp-sci superpower, all manner of hard tasks become trivial. All the locks on public-key encrypted messages would open for you. The SSL on your bank website, the cypher on your cellphone or the new DVDs, a million hidden messages all made transparent. All kinds of people would step up to give you awards (and money, lots of money) in addition to all the prize money waiting for those who decrypt ciphers, such as offered by RSA and the EFF. Well worth thinking about a little, no matter how unlikely you are to crack it.